Pythonで「データ解析のための統計モデリング入門」:第5章
Pythonで緑本(「データ解析のための統計モデリング入門」)の演習をしていきます。前記事はこちら。
第5章は「GLMの尤度比検定と検定の非対称性」ということで、統計モデルの逸脱度の差に注目する尤度比検定についてです。
統計モデルの検定における「帰無仮説・対立仮説」が、AICによるモデル選択では「単純モデル・複雑モデル」となります。一定モデル(単純モデル)とxモデル(複雑モデル)の逸脱度の差が例えば4.5だったとして、尤度比検定では、検定統計量であるこの逸脱度の差が「4.5ぐらいでは改善されていない」と言ってよいのかどうかを調べます。逸脱度の差は以下の式で表せます
\[ \Delta D_{1,2} = -2 \times (\log L_{1} – \log L_{2}) \]
検定の全体の流れは以下のようになります。
(1)まずは帰無仮説である一定モデルが正しいものだと仮定する
(2)観測データに一定モデルをあてはめると、 (\hat{\beta_{1}} = 2.06 ) となったので、これは真のモデルとほぼ同じと考えよう
(3)この真のモデルからデータを何度も生成し、そのたびに ( \beta_{2} = 0 (k = 1) ) と( \beta_{2}\neq 0 (k = 2) ) のモデルをあてはめれば、たくさんの ( \Delta D_{1,2} ) が得られるから、 ( \Delta D_{1,2} ) の分布がわかるだろう
(4)そうすれば、一定モデルとxモデルの逸脱度の差が( \Delta D_{1,2}\ge 4.5 )となる確率 ( P ) が評価できるだろう
5.4.1 方法(1) 汎用性のあるパラメトリックブートストラップ法
パラメトリックブートストラップ法は、前述した検定の流れの(3)における「データを何度も生成し」の仮定を、乱数発生のシミュレーションによって実施する方法です。
この章の例題データのGLMによる推定結果は、一定モデルとxモデルそれぞれfit1とfit2に格納されているとします。
一定モデルとxモデルの逸脱度の差 ( \Delta D_{1,2}\ge 4.5 ) を計算します。
from __future__ import division, print_function, absolute_import, unicode_literals
import pandas as pd
d = pd.read_csv('data/data3a.csv')
import statsmodels.api as sm
import statsmodels.formula.api as smf
fit1 = smf.glm(formula='y ~ 1', data=d, family=sm.families.Poisson()).fit()
fit2 = smf.glm(formula='y ~ x', data=d, family=sm.families.Poisson()).fit()
print(fit1.deviance - fit2.deviance)
4.51394107885
真のモデルから100個体ぶんのデータを新しく生成し、一定モデルとxモデルをこの新データにあてはめてみます。
import numpy as np d['y_rnd'] = np.random.poisson(d.y.mean(), 100) fit1 = smf.glm(formula='y_rnd ~ 1', data=d, family=sm.families.Poisson()).fit() fit2 = smf.glm(formula='y_rnd ~ x', data=d, family=sm.families.Poisson()).fit() print(fit1.deviance - fit2.deviance) 0.938292290633
今回は、逸脱度の差が0.94となりました。この1ステップによって「一定モデルが真のモデルである世界」での逸脱度の差がひとつ得られます。このステップを1000回ほど繰り返すと、「統計検定量の分布」、この例題でいうと「逸脱度の差 ( \Delta D_{1,2} ) の分布」を予測できます。
このPB法を実行するために、自作関数pb()を定義します。
def get_dd(d):
d['y_rnd'] = np.random.poisson(d.y.mean(), len(d.y))
fit1 = smf.glm(formula='y_rnd ~ 1', data=d, family=sm.families.Poisson()).fit()
fit2 = smf.glm(formula='y_rnd ~ x', data=d, family=sm.families.Poisson()).fit()
return fit1.deviance - fit2.deviance
def pb(d, n_bootstrap):
return pd.Series([get_dd(d) for i in range(n_bootstrap)])
dd12 = pb(d, 1000)
以上の操作によって、逸脱度の差 ( \Delta D_{1,2} ) のサンプルが1000個つくられてdd12に格納されました。実は ( \Delta D_{1,2} ) のサンプル個数は ( 10^3 ) ぐらいでは十分ではなく、( 10^4 ) かそれ以上にしたほうが良いとのことです。
概要を調べます。
print(dd12.describe()) count 1000.000000 mean 0.983494 std 1.508326 min 0.000002 25% 0.092785 50% 0.456521 75% 1.259388 max 16.785845 dtype: float64
ヒストグラムで図示、そして逸脱度の差が4.5がどのあたりにくるのかを示します。
import matplotlib.pyplot as plt
fig = plt.figure()
ax = fig.add_subplot(111)
ax.hist(dd12, 100)
ax.set_xlabel(r'$\Delta D_{1,2}$')
plt.axvline(x=4.5, linestyle='--')
fig.savefig("itsudatsu.png")
plt.close(fig)
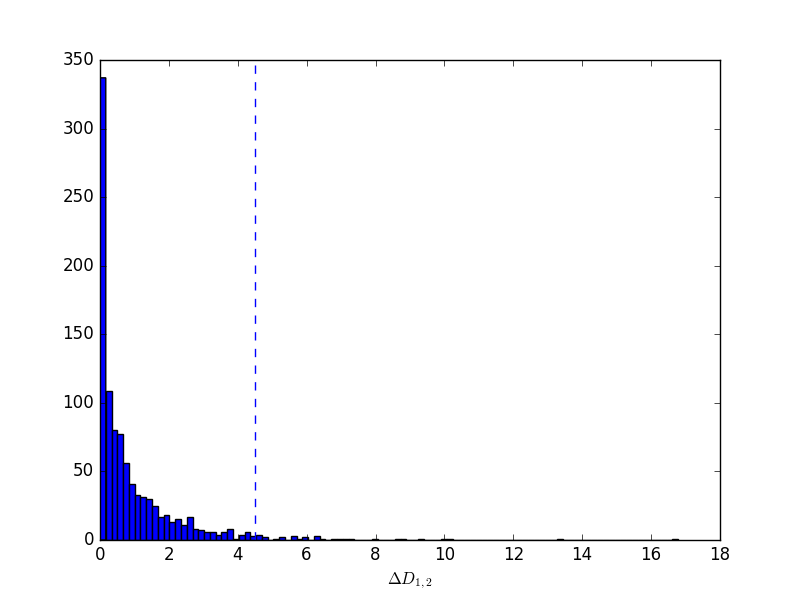
合計1000個ある ( \Delta D_{1,2} ) のうちいくつぐらいが、この4.5より右にあるのでしょうか?
print((dd12 >= 4.5).sum()) 31
1000個中の31個が4.5より大きい、つまり確率は31/1000、すなわち ( P = 0.0031 ) ということになります。ついでに、( P = 0.05 ) となる逸脱度の差 ( \Delta D_{1,2} ) を調べてみると、
print(dd12.quantile(0.95)) 3.77686899182
となり、有意水準5%の統計学的検定のわくぐみのもとでは、 ( \Delta D_{1,2}\leq 3.78) ぐらいまでは「よくある差」とみなされます。
この尤度比検定の結論としては、「逸脱度の差4.5の ( P ) 値は0.031だったので、これは有意水準0.05よりも小さい」ので有意差が有り、「帰無仮説(一定モデル)は棄却され、xモデルが残るのでこれを採択」と判断します。
5.4.2 方法(2) \( \chi^2 \) 分布を使った近似計算法
近似計算法を使うと、もっとお手軽に尤度比検定ができる場合があります。
逸脱度の差 ( \Delta D_{1,2} ) の確率分布は、自由の1の ( \chi^2 ) 分布に近似できる場合があります。Rではanova()関数を使い、anova(fit1, fit2, test=”Chisq”) といったふうにすれば ( P ) 値が得られますが、statsmodelsのanova関数(statsmodels.stats.anova.anova_lm())はGLMの結果に対応していません。
ですが、つまり5.4.1で得た逸脱度の差の確率分布を自由の1の ( \chi^2 ) 分布に近似して作って、その後は同様に計算すればいけるってことですよね・・・?
fit1 = smf.glm(formula='y ~ 1', data=d, family=sm.families.Poisson()).fit() fit2 = smf.glm(formula='y ~ x', data=d, family=sm.families.Poisson()).fit() chi = pd.Series(np.random.chisquare(1, 1000)) print((chi >= 4.5).sum() / 1000) print(chi.quantile(0.95)) 0.036 3.99139774575
得られた( P ) 値は0.0036です。ただ、( \chi^2 ) 分布近似はサンプルサイズが大きい場合に有効な近似計算なので、( P ) 値はあまり正確ではない可能性があります。
調査した個体数が多くない小標本のもとでは、PB法を使って逸脱度差の分布をシミュレーションで生成するのがいいでしょう、とのことです。

This Post Has 0 Comments