私の研究テーマの1つに、音が明瞭に聞こえる室内空間の特徴の解明というものがあります。ざっくり言ってしまうと、「部屋の音響的な物理特性」と「人間の聴感印象」との関係をモデル化することが最終的な目標です。

しかしモデル化の手法などについて勉強不足なものですから、研究室の院生で集まって、現在界隈で大人気と言われている久保拓弥先生の緑本を読み進める勉強会を始めました。

本の中の演習ではRが使用されていますが、私はお気に入りのPythonでやってみることにしました。ググると既にPythonでやってみた系の投稿が大量に出てきましたので、私の記事自体にほとんど意味は無いですが、自分のメモ代わりに。

また、当然ですが内容全てを網羅している訳ではないためご了承ください。

第2章　確率分布と統計モデルの最尤推定

まず、統計モデルとはそもそも何？という話は、まさに著者の久保先生がアップされてるスライドがとっても分かりやすいです。

一般化線形モデル (GLM) の基礎　統計モデルって何だろう?

第2章は統計モデルで重要な「確率分布」についてです。

2.1　例題：種子数の統計モデリング

本章で扱っているサンプルデータは、架空の植物50個体からなる集団を調査して得られた各個体の種子数を数えたものです。

サンプルデータ（.RData）はこちらからダウンロードできます。Pythonでこれを読み込むには、pyperを使います。pyperについては是非私の過去記事をご参照ください。

後の分析で色々と便利なので、読み込んだデータをpandasのSeriesに格納します。

from __future__ import division, print_function, absolute_import, unicode_literals
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import pyper as pr
from scipy import stats

r = pr.R(use_numpy='True', use_pandas='True')
r('load("/Users/作業ディレクトリ/data.RData")')
data = pd.Series(r.get('data'))

# 結果
print(data)

0     2
1     2
2     4
3     6
4     4
5     5
6     2
7     3
8     1
9     2
10    0
11    4
12    3
13    3
14    3
15    3
16    4
17    2
18    7
19    2
20    4
21    3
22    3
23    3
24    4
25    3
26    7
27    5
28    3
29    1
30    7
31    6
32    4
33    6
34    5
35    2
36    4
37    7
38    2
39    2
40    6
41    2
42    4
43    5
44    4
45    5
46    1
47    3
48    2
49    3
dtype: int64

データ数の確認。

print(len(data))

50

Series.describe()メソッドで標本平均、最小値、最大値、四分位数の算出。

print(data.describe())

count    50.00000
mean      3.56000
std       1.72804
min       0.00000
25%       2.00000
50%       3.00000
75%       4.75000
max       7.00000
dtype: float64

Series.value_counts()メソッドで度数分布を得る。

print(data.value_counts(sort=False))

3    12
2    11
4    10
5     5
7     4
6     4
1     3
0     1
dtype: int64

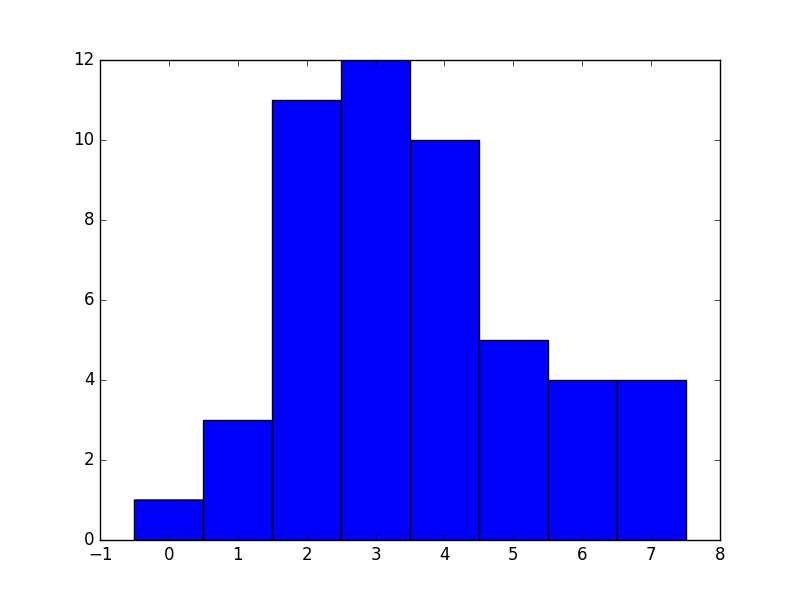
ヒストグラムとして図示する。

plt.hist(data, bins=np.arange(-0.5, 8.5, 1.0))
plt.savefig('hist.pdf')

データのばらつきを表す標本統計量の一つである標本分散の算出。

print(data.var())

2.98612244898

標本分散の平方根である標本標準偏差の算出。numpyのsqrt関数を使います。

print(np.sqrt(data.var()))

1.72804006

2.2　データと確率分布の対応関係をながめる

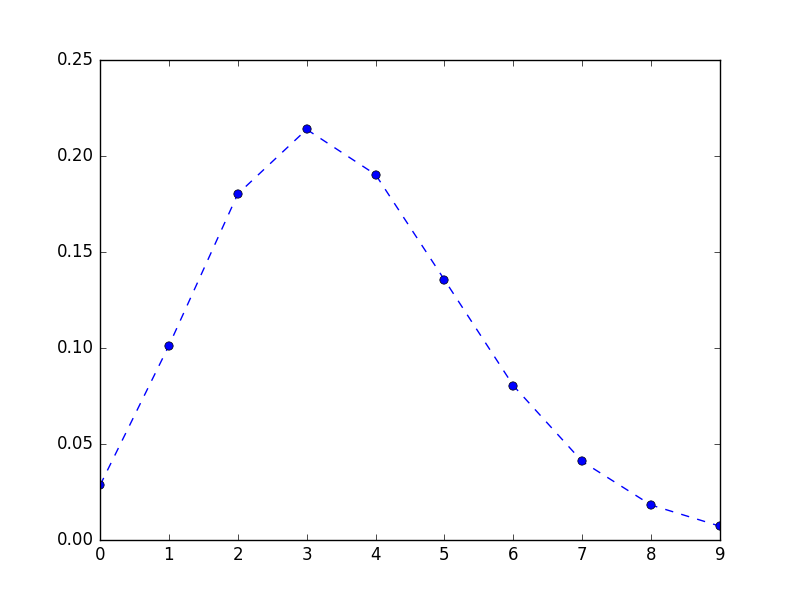
平均3.56のポアソン分布にしたがって「ある個体の種子数がy個である確率」を表形式で出力します。scipyのstatsを使います。プロットに便利なのでやはりpandasのSeriesに格納します。

y = np.arange(0, 10)
prob = pd.Series(stats.poisson.pmf(y, 3.56), index=y)

print(prob)

0    0.028439
1    0.101242
2    0.180211
3    0.213851
4    0.190327
5    0.135513
6    0.080404
7    0.040891
8    0.018197
9    0.007198
dtype: float64

折れ線グラフで図示します。

plt.plot(prob, 'o--')
plt.savefig('poisson.png')

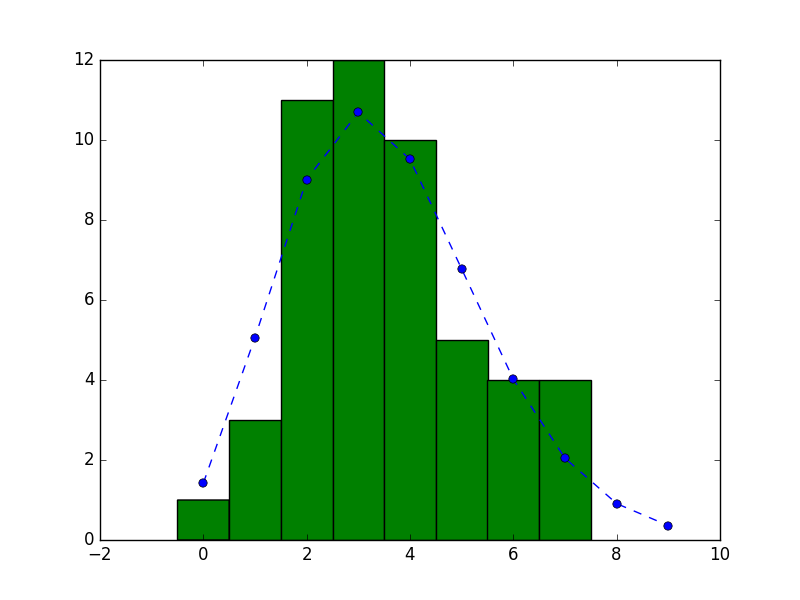
観測データのヒストグラムに平均3.56のポアソン分布を重ねます。

plt.plot(prob * 50, 'o--')
plt.hist(data, bins=np.arange(-0.5, 8.5, 1.0))
plt.savefig('hist_poisson.png')

2.3　ポアソン分布とは何か？

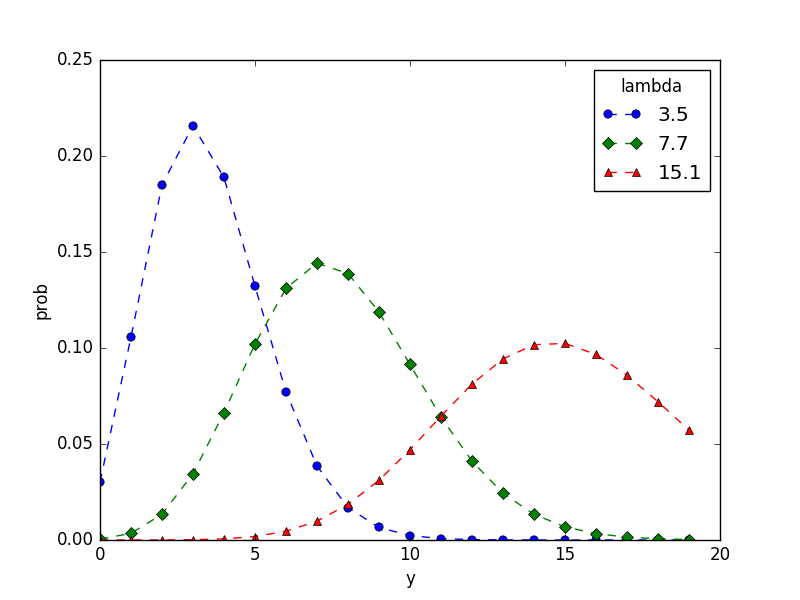
ポワソン分布の確率分布は以下のように定義されます。

\[ p(y|\lambda) = \frac{\lambda^y \exp(-\lambda)}{y!} \]

( p(y|\lambda) ) は平均が( \lambda )であるときに、ポアソン分布にしたがう確率変数が yという値になる確率です。ポアソン分布のパラメータ( \lambda )を変えると、以下のように確率分布が変化します。

y = np.arange(0, 20)
plt.plot(pd.Series(stats.poisson.pmf(y, 3.5), index=y), 'o--', label=3.5)
plt.plot(pd.Series(stats.poisson.pmf(y, 7.7), index=y), 'D--', label=7.7)
plt.plot(pd.Series(stats.poisson.pmf(y, 15.1), index=y), '^--', label=15.1)
plt.legend(loc='upper right', title='lambda')
plt.xlabel('y')
plt.ylabel('prob')
plt.savefig('hoge.png')

2.4　ポアソン分布のパラメーターの最尤推定

最尤推定法は、確率分布のパラメーターを、観測データにもとづいて推定する方法の一つです。

最尤推定法は、尤度なる「あてはまりの良さ」をあらわす統計量を最大にするようなパラメーター（ここではλ）の値を探そうとするパラメーター推定法で、ここでの尤度とは、ある( \lambda )の値を決めた時にすべての個体iについての( p(yi | \lambda) )の積になります。

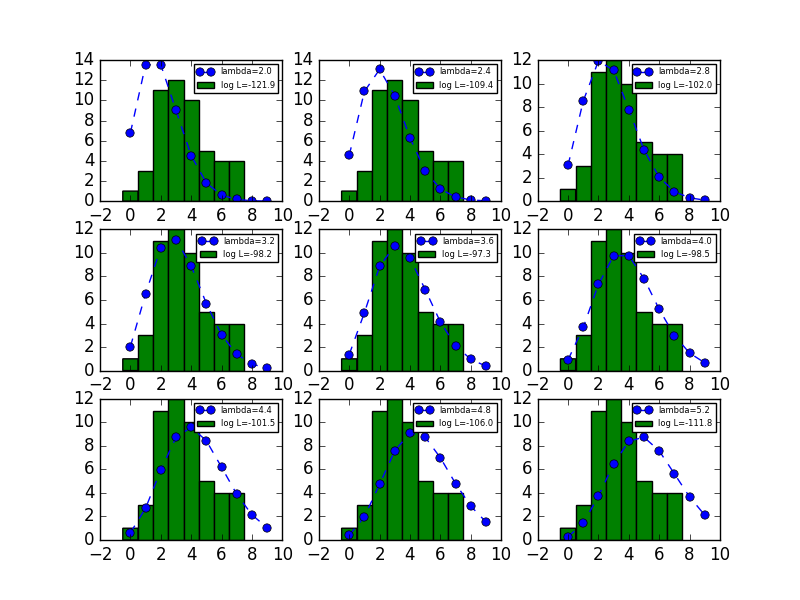
例題で、平均を表すパラメーター( \lambda )を変化させていったときに、ポアソン分布の形と対数尤度がどのように変化するかを表示します。

y = np.arange(0, 10)

fig = plt.figure()

ax1 = fig.add_subplot(331)
t_lambda = 2.0
ax1.plot(pd.Series(stats.poisson.pmf(y, t_lambda), index=y) * 50, 'o--', label='lambda=%.1f' % t_lambda)
ax1.hist(data, bins=np.arange(-0.5, 8.5, 1.0), label='log L=%.1f' % sum(stats.poisson.logpmf(data, t_lambda)))
ax1.legend(loc='upper right', fontsize=6)

ax2 = fig.add_subplot(332)
t_lambda = 2.4
ax2.plot(pd.Series(stats.poisson.pmf(y, t_lambda), index=y) * 50, 'o--', label='lambda=%.1f' % t_lambda)
ax2.hist(data, bins=np.arange(-0.5, 8.5, 1.0), label='log L=%.1f' % sum(stats.poisson.logpmf(data, t_lambda)))
ax2.legend(loc='upper right', fontsize=6)

ax3 = fig.add_subplot(333)
t_lambda = 2.8
ax3.plot(pd.Series(stats.poisson.pmf(y, t_lambda), index=y) * 50, 'o--', label='lambda=%.1f' % t_lambda)
ax3.hist(data, bins=np.arange(-0.5, 8.5, 1.0), label='log L=%.1f' % sum(stats.poisson.logpmf(data, t_lambda)))
ax3.legend(loc='upper right', fontsize=6)

ax4 = fig.add_subplot(334)
t_lambda = 3.2
ax4.plot(pd.Series(stats.poisson.pmf(y, t_lambda), index=y) * 50, 'o--', label='lambda=%.1f' % t_lambda)
ax4.hist(data, bins=np.arange(-0.5, 8.5, 1.0), label='log L=%.1f' % sum(stats.poisson.logpmf(data, t_lambda)))
ax4.legend(loc='upper right', fontsize=6)

ax5 = fig.add_subplot(335)
t_lambda = 3.6
ax5.plot(pd.Series(stats.poisson.pmf(y, t_lambda), index=y) * 50, 'o--', label='lambda=%.1f' % t_lambda)
ax5.hist(data, bins=np.arange(-0.5, 8.5, 1.0), label='log L=%.1f' % sum(stats.poisson.logpmf(data, t_lambda)))
ax5.legend(loc='upper right', fontsize=6)

ax6 = fig.add_subplot(336)
t_lambda = 4.0
ax6.plot(pd.Series(stats.poisson.pmf(y, t_lambda), index=y) * 50, 'o--', label='lambda=%.1f' % t_lambda)
ax6.hist(data, bins=np.arange(-0.5, 8.5, 1.0), label='log L=%.1f' % sum(stats.poisson.logpmf(data, t_lambda)))
ax6.legend(loc='upper right', fontsize=6)

ax7 = fig.add_subplot(337)
t_lambda = 4.4
ax7.plot(pd.Series(stats.poisson.pmf(y, t_lambda), index=y) * 50, 'o--', label='lambda=%.1f' % t_lambda)
ax7.hist(data, bins=np.arange(-0.5, 8.5, 1.0), label='log L=%.1f' % sum(stats.poisson.logpmf(data, t_lambda)))
ax7.legend(loc='upper right', fontsize=6)

ax8 = fig.add_subplot(338)
t_lambda = 4.8
ax8.plot(pd.Series(stats.poisson.pmf(y, t_lambda), index=y) * 50, 'o--', label='lambda=%.1f' % t_lambda)
ax8.hist(data, bins=np.arange(-0.5, 8.5, 1.0), label='log L=%.1f' % sum(stats.poisson.logpmf(data, t_lambda)))
ax8.legend(loc='upper right', fontsize=6)

ax9 = fig.add_subplot(339)
t_lambda = 5.2
ax9.plot(pd.Series(stats.poisson.pmf(y, t_lambda), index=y) * 50, 'o--', label='lambda=%.1f' % t_lambda)
ax9.hist(data, bins=np.arange(-0.5, 8.5, 1.0), label='log L=%.1f' % sum(stats.poisson.logpmf(data, t_lambda)))
ax9.legend(loc='upper right', fontsize=6)

fig.savefig('lambdas.png')
plt.close(fig)

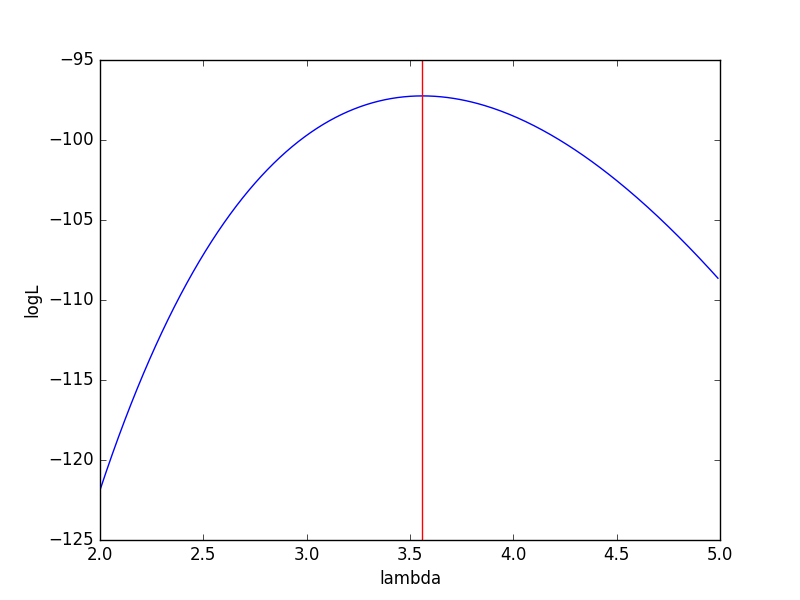
横軸にλ、縦軸に対数尤度をとったグラフを書きます。( \lambda = 3.56 )で対数尤度が最大になるので、これが最尤推定値となります。

y = np.arange(2.0, 5.0, 0.01)
logL = np.array([sum(stats.poisson.logpmf(data, i)) for i in y])
plt.plot(y, logL)
plt.axvline(x=y[np.argmax(logL)], color='red')
plt.xlabel('lambda')
plt.ylabel('logL')
plt.savefig('max_likelihood.png')