Pythonで「データ解析のための統計モデリング入門」:第3章
Pythonで緑本の演習をしていきます。前記事はこちら。
第3章、説明変数をくみこんだ統計モデルについてです。
第3章 一般化線形モデル(GLM)
第2章で使用したサンプルデータは、架空の植物50個体からなる集団を調査して得られた各個体の種子数を数えたものでした。このデータで、個体ごとに異なる説明変数(個体の属性)によって平均種子数が変化する統計モデルを観測データにあてはめることを、一般化線形モデル(GLM)と言います。
第3章では、一般化線形モデルの中のポアソン回帰を実施します。
3.1 例題:個体ごとに平均種子数が異なる場合
第3章の例題では、架空の植物100個体を調査して得られた、個体ごとの種子数のデータを用います。植物個体iの種子数は ( y_{i} ) 個であり、個体の属性のひとつである体サイズ ( x_{i} ) が観測されているとします。また、全個体のうち50個体は何も処理をしておらず、残り50個体には肥料を加える処理(処理T)をほどこしているとします。
3.2 観測されたデータの概要を調べる
サンプルデータ(csvファイル)はこちらからダウンロードできます。pandasのread_csvを使ってDataFrame形式で読み込みます。
# -*- coding:utf-8 -*-
"""
kubo_3.py
"""
from __future__ import division, print_function, absolute_import, unicode_literals
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from scipy import stats
d = pd.read_csv('data/data3a.csv')
print(d)
y x f
0 6 8.31 C
1 6 9.44 C
2 6 9.50 C
3 12 9.07 C
4 10 10.16 C
5 4 8.32 C
6 9 10.61 C
7 9 10.06 C
8 9 9.93 C
9 11 10.43 C
.. .. ... ..
90 6 11.20 T
91 5 9.86 T
92 8 11.54 T
93 5 10.03 T
94 9 11.88 T
95 8 9.15 T
96 6 8.52 T
97 8 10.24 T
98 7 10.86 T
99 9 9.97 T
dの列ごとにデータを表示させてみます。
print(d.x)
0 8.31
1 9.44
2 9.50
3 9.07
4 10.16
5 8.32
6 10.61
7 10.06
8 9.93
9 10.43
...
90 11.20
91 9.86
92 11.54
93 10.03
94 11.88
95 9.15
96 8.52
97 10.24
98 10.86
99 9.97
print(d.y)
0 6
1 6
2 6
3 12
4 10
5 4
6 9
7 9
8 9
9 11
..
90 6
91 5
92 8
93 5
94 9
95 8
96 6
97 8
98 7
99 9
print(d.f)
0 C
1 C
2 C
3 C
4 C
5 C
6 C
7 C
8 C
9 C
..
90 T
91 T
92 T
93 T
94 T
95 T
96 T
97 T
98 T
99 T
pandasのinfo()メソッドで各列のデータの型について知ることができます。
print(d.info()) <class 'pandas.core.frame.DataFrame'> Int64Index: 100 entries, 0 to 99 Data columns (total 3 columns): y 100 non-null int64 x 100 non-null float64 f 100 non-null object dtypes: float64(1), int64(1), object(1) memory usage: 3.1+ KB
describe()メソッドでデータの概要を示します。
print(d.describe())
y x
count 100.000000 100.000000
mean 7.830000 10.089100
std 2.624881 1.008049
min 2.000000 7.190000
25% 6.000000 9.427500
50% 8.000000 10.155000
75% 10.000000 10.685000
max 15.000000 12.400000
print(d.f.describe())
count 100
unique 2
top T
freq 50
Name: f, dtype: object
value_counts()メソッドで ( f )\ の要素の数を得られます。
print(d.f.value_counts()) T 50 C 50 Name: f, dtype: int64
3.3 統計モデリングの前にデータを図示する
まずは観測データに余計な手を加えないで、データ全体を見てみます。
横軸に ( x ) 列、縦軸に ( y ) 列をとった散布図をプロットします。
pandasのプロット機能を使っても良いかと思ったのですが(簡単に書ける場合が多い)、後々複雑なプロットをしたいと思った時を考えて、はじめからmatplotlibでいきます。
fig = plt.figure()
ax = fig.add_subplot(111)
ax.scatter(d.x[d.f=='C'], d.y[d.f=='C'], label='C', facecolors='none')
ax.scatter(d.x[d.f=='T'], d.y[d.f=='T'], label='T')
ax.legend(loc='upper left')
fig.savefig('scatter.png')
plt.close(fig)
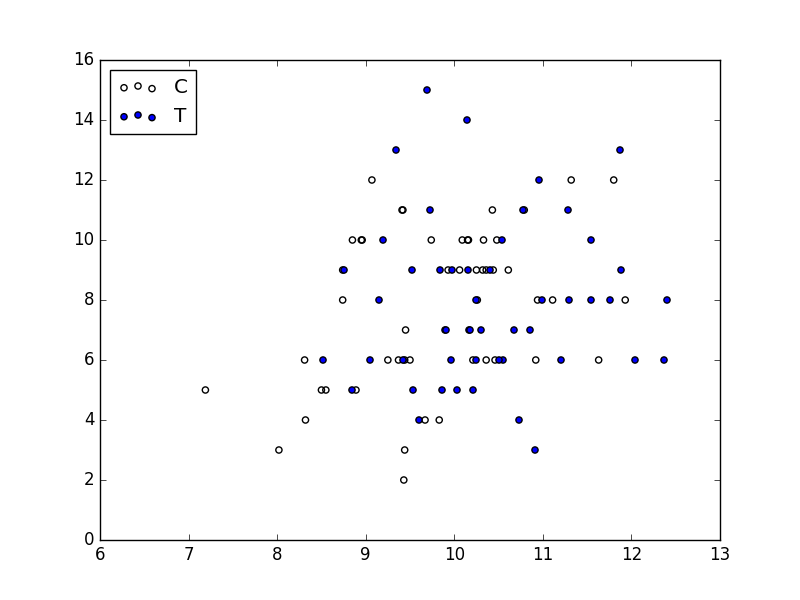
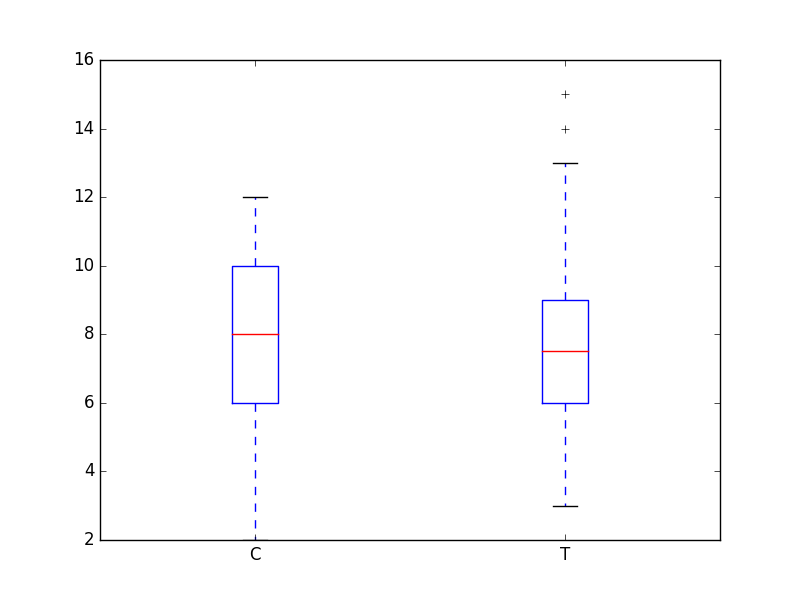
次に、横軸を施肥処理、縦軸に ( y ) 列をとった箱ひげ図をプロットします。
fig = plt.figure()
ax = fig.add_subplot(111)
ax.boxplot([d.y[d.f=='C'], d.y[d.f=='T']], labels=['C', 'T'])
fig.savefig('box_plot.png')
plt.close(fig)
3.4 ポアソン回帰の統計モデル
個体ごとの平均種子数 ( \lambda_{i} ) が体サイズ ( x ) や施肥処理 ( f ) に影響されるようなモデルを設計します。
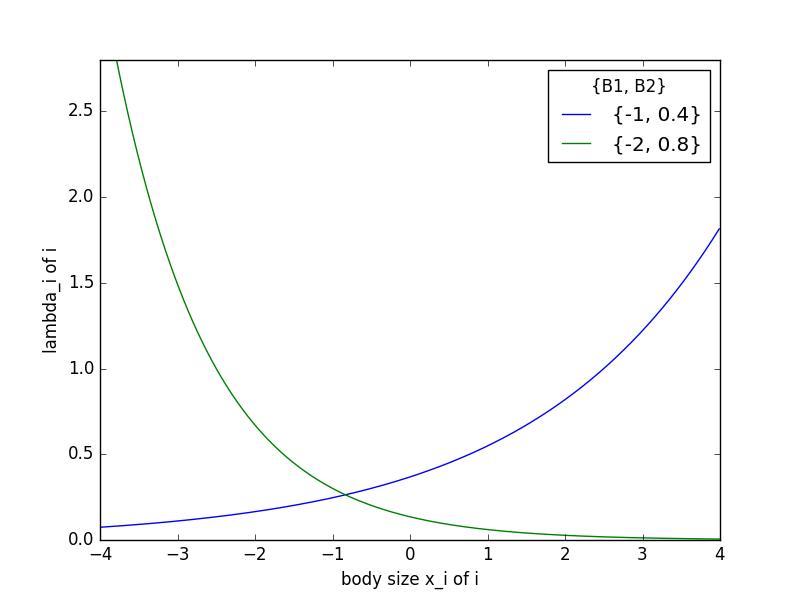
まず、個体 ( i ) の体サイズ ( x_{i} ) だけに依存する統計モデルについて考えます。切片 ( \beta_{1} ) 、 傾き ( \beta_{2} ) の関係を図示すると次のようになります。
x = np.arange(-4, 4, 0.01)
fig = plt.figure()
ax = fig.add_subplot(111)
ax.plot(x, np.exp(-1 + 0.4 * x), label='{-1, 0.4}')
ax.plot(x, np.exp(-2 + -0.8 * x), label='{-2, 0.8}')
ax.legend(title='{B1, B2}')
ax.set_ylim(0, 2.8)
ax.set_xlabel('body size x_i of i')
ax.set_ylabel('lambda_i of i')
fig.savefig('test.png')
plt.close(fig)
3.4.2 あてはめとあてはまりの良さ
ポアソン回帰とは、観測データに対するポアソン分布を使った統計モデルのあてはめであり、この統計モデルの対数尤度 ( \log L ) が最大になるパラメータ ( \hat{\beta}{1} ) と ( \hat{\beta}{2} ) の推定値を決めることです。
Rではglm()関数を使うことで手軽にGLMのあてはめができます。pythonでやる方法をググッてみたら、scikit-learnやstatsmodelsというモジュールが有名なようです。statsmodelsはRライクに使えるとのことで、ここではstatsmodelでやってみます。
調べてみると、Statsmodelsには通常の関数型呼び出しに対応するAPIと、R-styleのモデル式を用いる数式対応API(formula API)の2種類が実装されているとのことでした。
Statsmodels formula API と多項式回帰モデル
以下のようにして切片 \( \hat{\beta}_{1} \) と \( \hat{\beta}_{2} \) の推定値を求めてみました。GLMはformula APIで実行し、ポアソン分布の指定に通常のAPIを使っています。Rのように、formulaの指定を’従属変数 ~ 説明変数’という風に指定できました。
import statsmodels.api as sm import statsmodels.formula.api as smf fit = smf.glm(formula='y ~ x', data=d, family=sm.families.Poisson()) print(fit.fit().summary())
Generalized Linear Model Regression Results
==============================================================================
Dep. Variable: y No. Observations: 100
Model: GLM Df Residuals: 98
Model Family: Poisson Df Model: 1
Link Function: log Scale: 1.0
Method: IRLS Log-Likelihood: -235.39
Date: Tue, 10 May 2016 Deviance: 84.993
Time: 18:18:59 Pearson chi2: 83.8
No. Iterations: 7
==============================================================================
coef std err z P>|z| [95.0% Conf. Int.]
------------------------------------------------------------------------------
Intercept 1.2917 0.364 3.552 0.000 0.579 2.005
x 0.0757 0.036 2.125 0.034 0.006 0.145
==============================================================================
3.4.3 ポアソン回帰モデルによる予測
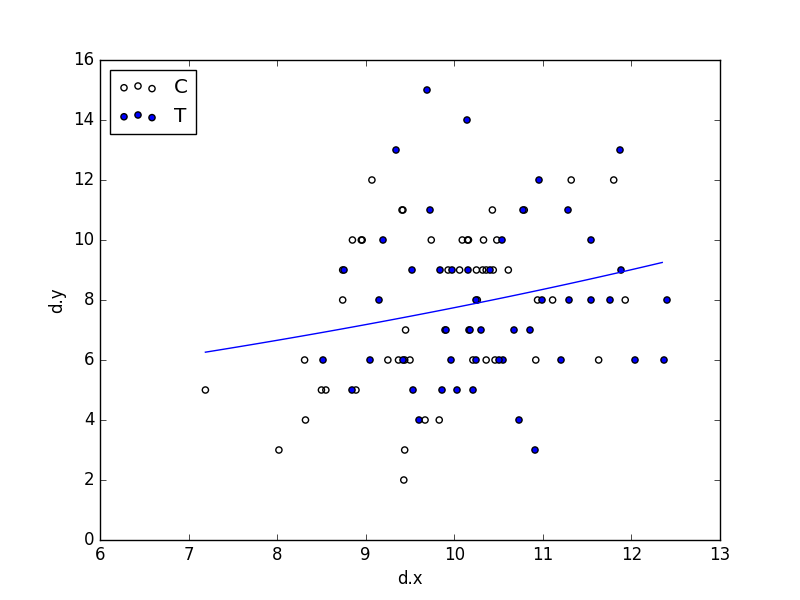
次に、このポアソン回帰の推定結果を使って、様々な体サイズ ( x ) における平均種子数 ( \lambda ) の予測を行います。
\[ \lambda = \exp (1.29 + 0.0757 x) \]
これを図示します。
fig = plt.figure()
ax = fig.add_subplot(111)
ax.scatter(d.x[d.f=='C'], d.y[d.f=='C'], label='C', facecolors='none')
ax.scatter(d.x[d.f=='T'], d.y[d.f=='T'], label='T')
xx = np.arange(min(d.x), max(d.x), (max(d.x) - min(d.x)) / 100)
ax.plot(xx, np.exp(1.29 + 0.0757 * xx))
ax.set_xlabel('d.x')
ax.set_ylabel('d.y')
ax.legend(loc='upper left')
fig.savefig('predict.png')
plt.close(fig)
3.5 説明変数が因子型の統計モデル
施肥効果 ( f_{i} ) を説明変数としてくみこんだモデルも検討します。施肥処理は因子型、カテゴリ型のデータとして格納されています。
Pythonで推定を行います。因子型の説明変数であっても、簡単にモデル式を指定できます。
import statsmodels.api as sm import statsmodels.formula.api as smf fit = smf.glm(formula='y ~ f', data=d, family=sm.families.Poisson()) print(fit.fit().summary())
Generalized Linear Model Regression Results
==============================================================================
Dep. Variable: y No. Observations: 100
Model: GLM Df Residuals: 98
Model Family: Poisson Df Model: 1
Link Function: log Scale: 1.0
Method: IRLS Log-Likelihood: -237.63
Date: Tue, 10 May 2016 Deviance: 89.475
Time: 19:19:42 Pearson chi2: 87.1
No. Iterations: 7
==============================================================================
coef std err z P>|z| [95.0% Conf. Int.]
------------------------------------------------------------------------------
Intercept 2.0516 0.051 40.463 0.000 1.952 2.151
f[T.T] 0.0128 0.071 0.179 0.858 -0.127 0.153
==============================================================================
3.6 説明変数が数量型 + 因子型の統計モデル
個体の体サイズ ( x_{i} ) と施肥効果 ( f_{i} ) の複数の説明変数を同時にくみこんだ統計モデルを作ってみます。
statsmodelでは、モデル式の部分をx + fとするだけで適切に処理してくれます。
import statsmodels.api as sm import statsmodels.formula.api as smf fit = smf.glm(formula='y ~ x + f', data=d, family=sm.families.Poisson()) print(fit.fit().summary())
Generalized Linear Model Regression Results
==============================================================================
Dep. Variable: y No. Observations: 100
Model: GLM Df Residuals: 97
Model Family: Poisson Df Model: 2
Link Function: log Scale: 1.0
Method: IRLS Log-Likelihood: -235.29
Date: Wed, 11 May 2016 Deviance: 84.808
Time: 13:32:13 Pearson chi2: 83.8
No. Iterations: 7
==============================================================================
coef std err z P>|z| [95.0% Conf. Int.]
------------------------------------------------------------------------------
Intercept 1.2631 0.370 3.417 0.001 0.539 1.988
f[T.T] -0.0320 0.074 -0.430 0.667 -0.178 0.114
x 0.0801 0.037 2.162 0.031 0.007 0.153
==============================================================================

This Post Has 0 Comments