Pythonで「データ解析のための統計モデリング入門」:第6章
Pythonで緑本(「データ解析のための統計モデリング入門」)の演習をしていきます。前記事はこちら。
今回は第6章。この章では、ポアソン分布以外の確率分布の統計モデル、そしてGLMのオフセット項の使いかたについて書かれています。
※書籍の内容全てを網羅している訳ではありません、自分なりの解釈でまとめております。
6.2 例題:上限のあるカウントデータ
二項分布は上限のあるカウントデータをあらわすために使います。
この例題では、ある架空植物の個体 ( i ) それぞれにおいて「 ( N_{i} ) 個の観察種子のうち生きていて発芽能力のあるものは ( y_{i} ) 、死んだ種子は ( N_{i} – y_{i} ) 個」といった観察データが得られたとします。ある個体( i ) から得られた1個の種子が生きている確率を、生存確率 ( q_{i} ) とします。
説明変数としては、個体の大きさをあらわす体サイズ ( x_{i} ) 、施肥処理の有無 ( f_{i} ) となります。ここで調べたいことは、ある個体の生存確率( q_{i} ) が ( x_{i} ) や ( f_{i} ) といった説明変数によってどう変化するのかという点です。
例題データはこちらからダウンロードしてください。
まず、各列のまとめを表示します。
from __future__ import division, print_function, absolute_import, unicode_literals
import pandas as pd
d = pd.read_csv('data/data4a.csv')
print(d.describe())
print(d.f.value_counts())
N y x count 100 100.000000 100.000000 mean 8 5.080000 9.967200 std 0 2.743882 1.088954 min 8 0.000000 7.660000 25% 8 3.000000 9.337500 50% 8 6.000000 9.965000 75% 8 8.000000 10.770000 max 8 8.000000 12.440000 T 50 C 50 Name: f, dtype: int64
散布図をプロットします。
import matplotlib.pyplot as plt
fig = plt.figure()
ax = fig.add_subplot(111)
ax.scatter(d.x[d.f=='C'], d.y[d.f=='C'], label='C', facecolors='none')
ax.scatter(d.x[d.f=='T'], d.y[d.f=='T'], label='T')
ax.legend(loc='upper left')
ax.set_xlabel('$x_{i}$')
ax.set_ylabel('$y_{i}$')
fig.savefig('scatter.png')
plt.close(fig)
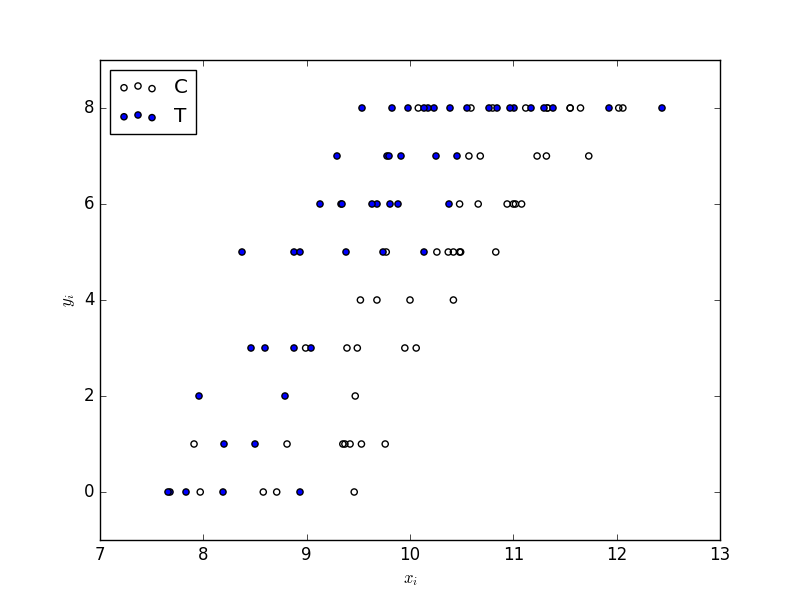
体サイズ ( x_{i} ) が大きくなると生存種子数 ( y_{i} ) が多くなるらしい。肥料をやると (( f_{i} = T )) 生存種子数 ( y_{i} ) が多くなるらしい。といったことが分かります。
6.3 二項分布で表現する「あり・なし」カウントデータ
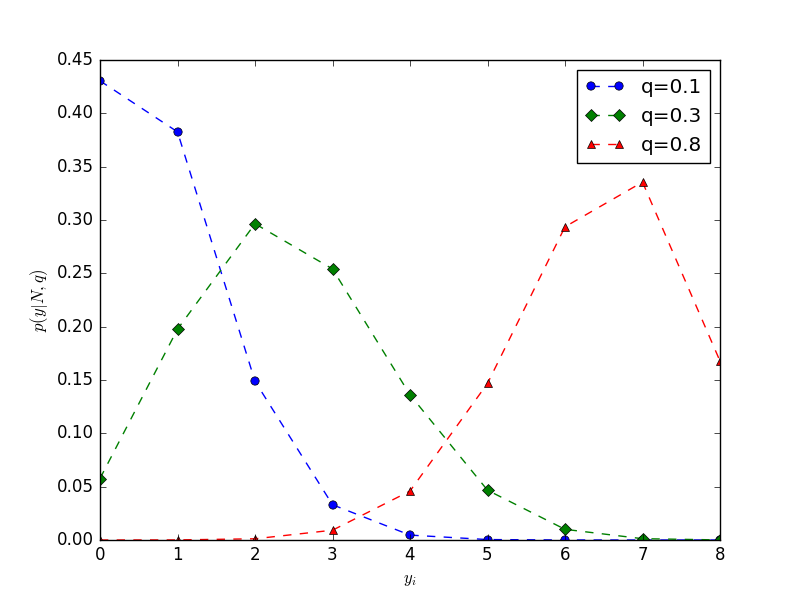
この例題のように、「 ( N ) 個のうち ( y ) 個が生存していた」といった構造のカウントデータを統計モデルで表現するときには、二項分布がよく使われています。
\(\left( \begin{array}{rr} N \\ y \\ \end{array} \right) \) は「場合の数」で、ここでは「\( N \) 個の観察種子の中から \( y \) 個の生存種子を選び出す場合の数」となります。
from scipy import stats
import numpy as np
y = np.arange(0, 9)
plt.plot(pd.Series(stats.binom.pmf(y, 8, 0.1), index=y), 'o--', label='q=0.1')
plt.plot(pd.Series(stats.binom.pmf(y, 8, 0.3), index=y), 'D--', label='q=0.3')
plt.plot(pd.Series(stats.binom.pmf(y, 8, 0.8), index=y), '^--', label='q=0.8')
plt.legend(loc='upper right')
plt.xlabel('$y_{i}$')
plt.ylabel('$p (y | N, q)$')
plt.savefig('binom.png')
6.4 ロジスティック回帰とロジットリンク関数
二項分布を使ったGLMのひとつであるロジスティック回帰の統計モデルについてです。
ロジスティック回帰では確率分布は二項分布、そしてリンク関数はロジットリンク関数を指定します。
ロジスティック関数の関数形は
\[ q_{i} = \rm{logistic} (z_{i}) = \frac{1}{1 + \exp (-z_{i})} \]
であり、変数 \( z_{i} \) は線形予測子 \( z_{i} = \beta_{1} + \beta_{2} x_{i} + \) …です。
作図してみます。
import numpy as np
def logistic(z):
return 1 / (1 + np.exp(-z))
fig = plt.figure()
ax = fig.add_subplot(111)
x = np.arange(-6, 6, 0.1)
ax.plot(x, logistic(x))
ax.set_xlabel('$z_{i}$')
ax.set_ylabel('$q$')
fig.savefig('logistic.png')
plt.close(fig)
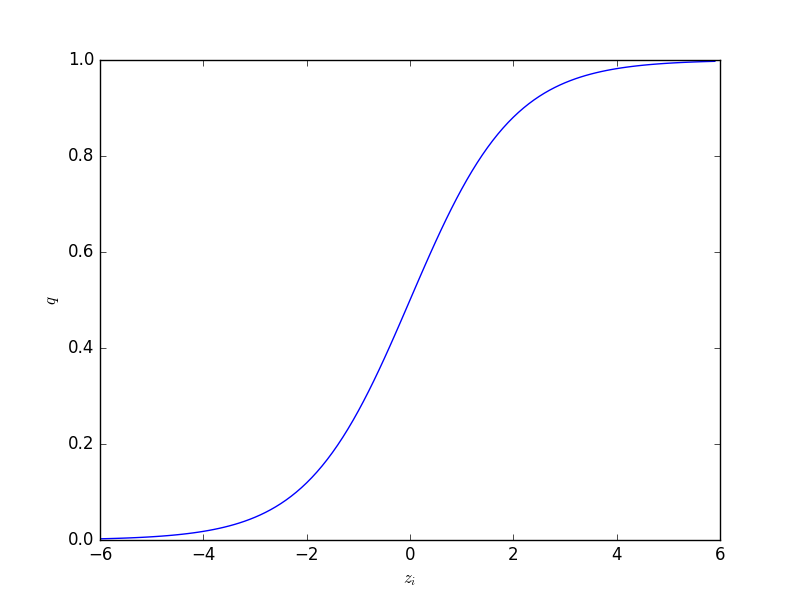
ロジスティック関数の逆関数であるロジット関数は次のようになります。
\[ \rm{logit} (q_{i}) = \log \frac{q_{i}}{1 – q_{i}} \]
この統計モデルをデータにあてはめてパラメーターを推定します。
Rでは目的変数にcbind(y, N-y)を取るようにしますが( \( y \) は生存していた種子数、 \( N-y \) は死んだ種子数)、statsmodelsでは、’y + I(N-y) ~ 説明変数’ のように記述することで実行できます。
import numpy as np import statsmodels.api as sm import statsmodels.formula.api as smf fit = smf.glm(formula='y + I(N - y) ~ x + f', data=d, family=sm.families.Binomial()) res_fit = fit.fit() print(res_fit.summary())
Generalized Linear Model Regression Results
==============================================================================
Dep. Variable: ['y', 'N_y'] No. Observations: 100
Model: GLM Df Residuals: 97
Model Family: Binomial Df Model: 2
Link Function: logit Scale: 1.0
Method: IRLS Log-Likelihood: -133.11
Date: Sat, 04 Jun 2016 Deviance: 123.03
Time: 17:26:31 Pearson chi2: 109.
No. Iterations: 8
==============================================================================
coef std err z P>|z| [95.0% Conf. Int.]
------------------------------------------------------------------------------
Intercept -19.5361 1.414 -13.818 0.000 -22.307 -16.765
f[T.T] 2.0215 0.231 8.740 0.000 1.568 2.475
x 1.9524 0.139 14.059 0.000 1.680 2.225
==============================================================================
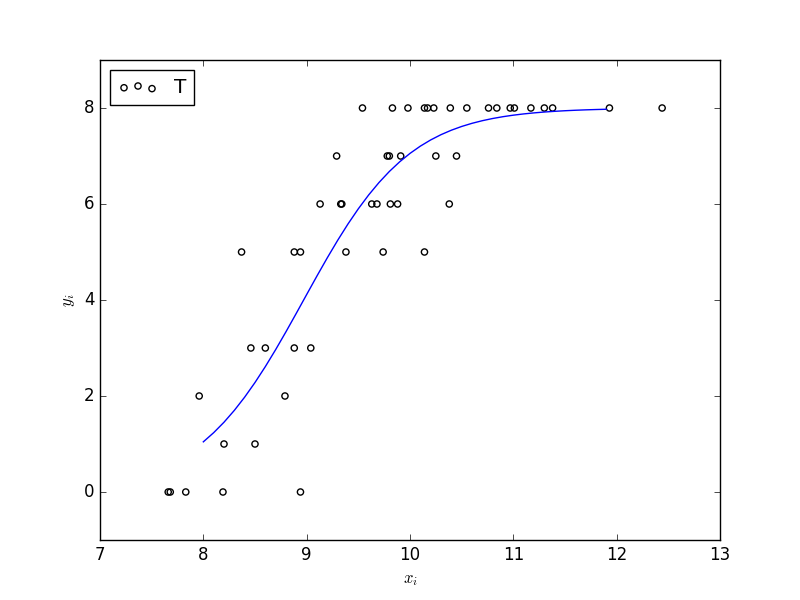
おおよそ ( { \hat{\beta_{1}},\hat{\beta_{2}}, \hat{\beta_{3}} } = {-19.5, 1.95, 2.02 } ) となっています。これらの推定値を使って、予測の曲線を書きます。ほぼほぼRのpredict()関数と同じように使えますね。
fig = plt.figure()
ax = fig.add_subplot(111)
ax.scatter(d.x[d.f=='T'], d.y[d.f=='T'], label='T', facecolors='none')
xx = np.arange(8, 12, 0.1)
yy = res_fit.predict(exog = pd.DataFrame({'x': xx, 'f': ['T'] * len(xx)}))
# ax.plot(xx, 1 / (1 + np.exp(- (-19.5 + (1.952 * xx) + 2.02))) * 8)
ax.plot(xx, yy * 8)
ax.set_xlabel('$x_{i}$')
ax.set_ylabel('$y_{i}$')
ax.legend(loc='upper left')
fig.savefig('predict.png')
plt.close(fig)
第4章で説明したAICによるモデル選択によって、これらのモデルの中から良い予測をするものを選びます。RであればMASS packageのstepAIC()関数というものを使えば、ネストしているモデルたちのAICを自動的に比較しながら、AIC最小のモデルを選択できるようですが、statsmodelsでは無いので、自力でやるしかなさそうです。
次に、交互作用を追加してみます。
fit = smf.glm(formula='y + I(N - y) ~ x * f', data=d, family=sm.families.Binomial()) res_fit = fit.fit() print(res_fit.summary()) print(res_fit.aic)
In [1]: Generalized Linear Model Regression Results
==============================================================================
Dep. Variable: ['y', 'I(N - y)'] No. Observations: 100
Model: GLM Df Residuals: 96
Model Family: Binomial Df Model: 3
Link Function: logit Scale: 1.0
Method: IRLS Log-Likelihood: -132.81
Date: Fri, 01 Jul 2016 Deviance: 122.43
Time: 12:23:12 Pearson chi2: 109.
No. Iterations: 8
==============================================================================
coef std err z P>|z| [95.0% Conf. Int.]
------------------------------------------------------------------------------
Intercept -18.5233 1.886 -9.821 0.000 -22.220 -14.827
f[T.T] -0.0638 2.704 -0.024 0.981 -5.363 5.235
x 1.8525 0.186 9.983 0.000 1.489 2.216
x:f[T.T] 0.2163 0.280 0.772 0.440 -0.333 0.765
==============================================================================
273.61059672597383
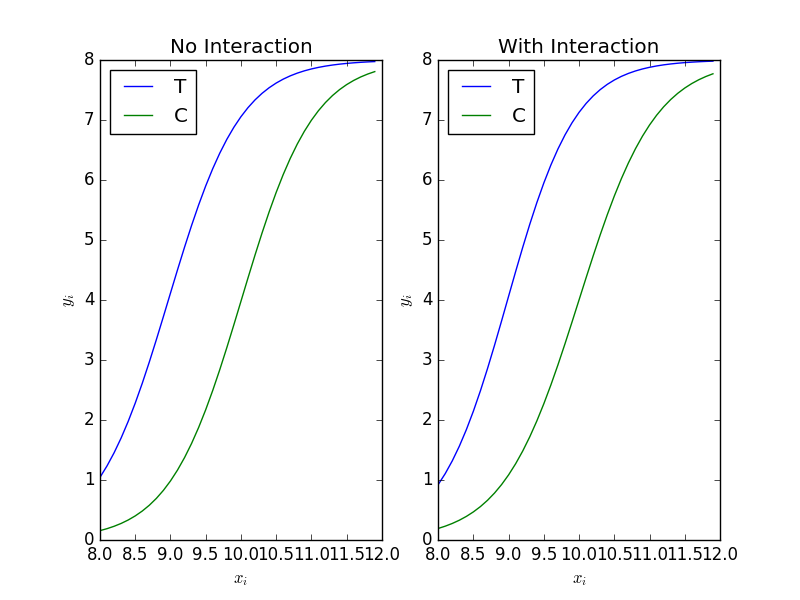
6.6 割算値の統計モデリングはやめよう
割算値、つまり変形した観測値を統計モデルの応答変数にするのは、不必要であるばかりでなく、まちがった結果を導きかねないものです。そこで、統計モデルを作る際にオフセット項わざを使います。
本では架空データを使ってポアソン回帰におけるオフセット項わざを説明していますが、ここでは省略してstatsmodelsの中のオフセット項の指定の方法だけ記述します。
import numpy as np fit = smf.glm(formula='y ~ x', offset=np.log(d['A']), data=d, family=sm.families.Poisson())
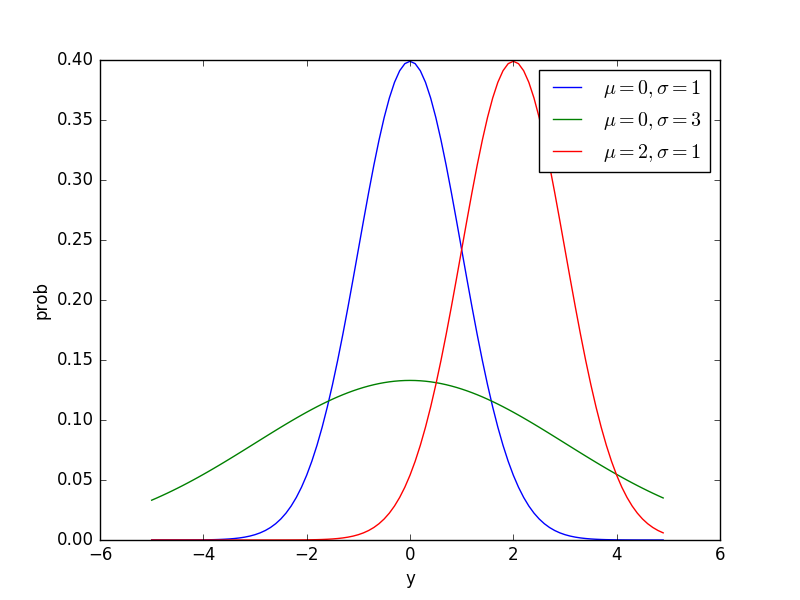
6.7 正規分布とその尤度
正規分布は連続値のデータを統計モデルであつかうための確率分布です。Pythonで正規分布の密度関数を図示してみます。
from scipy import stats
y = np.arange(-5, 5, 0.1)
plt.plot(pd.Series(stats.norm.pdf(y, loc=0, scale=1), index=y), label=r'$\mu=0, \sigma=1$')
plt.plot(pd.Series(stats.norm.pdf(y, loc=0, scale=3), index=y), label=r'$\mu=0, \sigma=3$')
plt.plot(pd.Series(stats.norm.pdf(y, loc=2, scale=1), index=y), label=r'$\mu=2, \sigma=1$')
plt.legend(loc='upper right')
plt.xlabel('y')
plt.ylabel('prob')
plt.savefig('Gaussian.png')
plt.close()
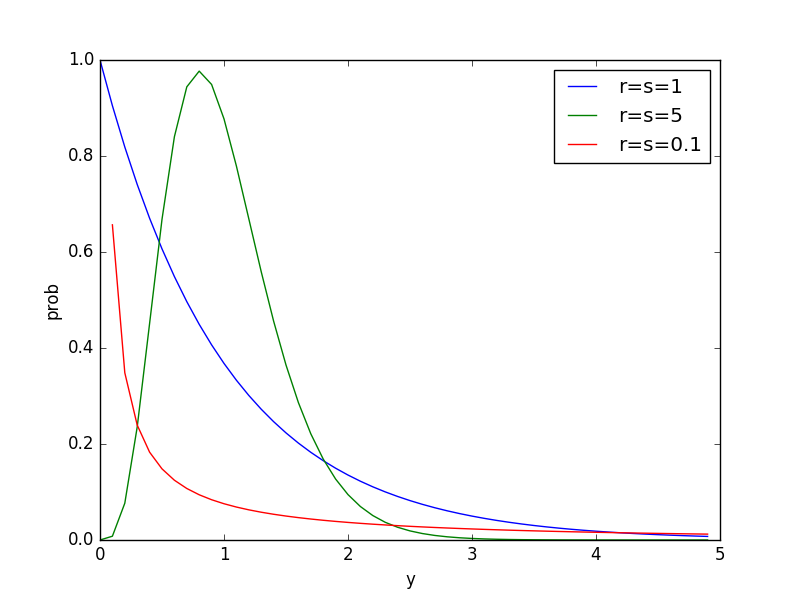
6.8 ガンマ分布のGLM
ガンマ分布は確率変数のとりうる範囲が0以上の連続確率分布です。
from scipy import stats
y = np.arange(0, 5, 0.1)
plt.plot(pd.Series(stats.gamma.pdf(y, 1, scale=1/(1**2)), index=y), label=r'r=s=1')
plt.plot(pd.Series(stats.gamma.pdf(y, 5, scale=5/(5**2)), index=y), label=r'r=s=5')
plt.plot(pd.Series(stats.gamma.pdf(y, 0.1, scale=0.1/(0.1**2)), index=y), label=r'r=s=0.1')
plt.legend(loc='upper right')
plt.xlabel('y')
plt.ylabel('prob')
plt.savefig('gamma.png')
plt.close()
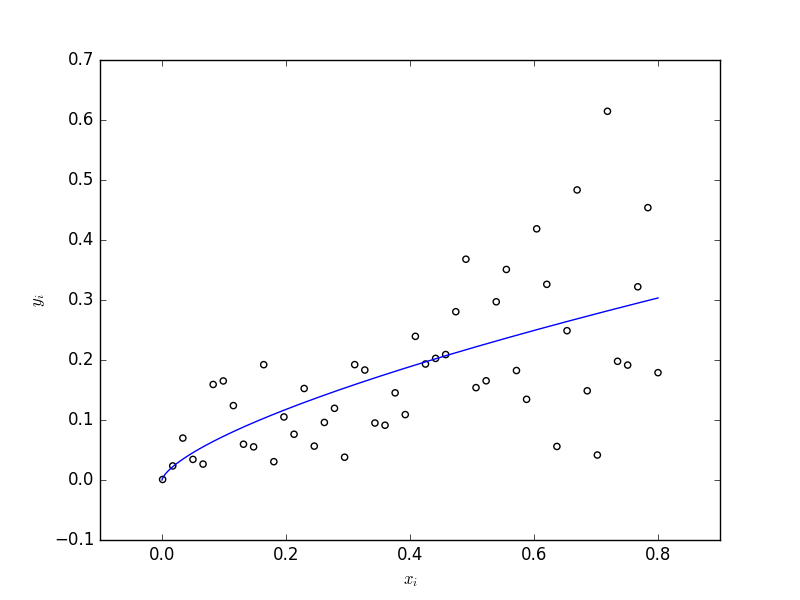
ガンマ関数を使ったGLMです。
import pyper as pr
r = pr.R(use_numpy='True', use_pandas='True')
r('load("data/d.RData")')
d = pd.DataFrame(r.get('d'))
d.columns = ['x', 'y']
d['logx'] = np.log(d.x)
fit = smf.glm(formula='y ~ logx', data=d, family=sm.families.Gamma(link=sm.families.links.log))
res_fit = fit.fit()
print(res_fit.summary())
Generalized Linear Model Regression Results
==============================================================================
Dep. Variable: y No. Observations: 50
Model: GLM Df Residuals: 48
Model Family: Gamma Df Model: 1
Link Function: log Scale: 0.325084605974
Method: IRLS Log-Likelihood: 58.471
Date: Tue, 12 Jul 2016 Deviance: 17.251
Time: 17:04:32 Pearson chi2: 15.6
No. Iterations: 12
==============================================================================
coef std err z P>|z| [95.0% Conf. Int.]
------------------------------------------------------------------------------
Intercept -1.0403 0.119 -8.759 0.000 -1.273 -0.808
logx 0.6832 0.068 9.992 0.000 0.549 0.817
==============================================================================
fig = plt.figure()
ax = fig.add_subplot(111)
ax.scatter(d.x, d.y, facecolors='none')
xx = pd.DataFrame({'x': np.linspace(0, 0.8, 1000)})
yy = res_fit.predict(xx)
ax.plot(xx, yy)
ax.set_ylabel("$y_i$")
ax.set_xlabel("$x_i$")
fig.savefig('graph.png')
plt.close(fig)

This Post Has 0 Comments